In the last piece of Expected Results, I presented a mathematical way to approach the desired number of lands for a Magic limited deck. That article focused on the number of lands only, without respect to varying combinations of different basic land types for multicolor decks.
Today I will discuss this second aspect of a mana base. In the first section I present a way to evaluate the quality of a multicolor mana base. The second section presents a web application that allows you to analyze any deck using the previously discussed approach.
Introductory Examples
Let me quickly explain my consideration about the right distribution of basic lands using a couple of my latest draft decks as examples.

My first consideration is the number of cards in each color in the deck. In this example the distribution of blue and white cards is even (11 white, 11 blue and 1 blue-white card). My conclusion is that the number of islands should be more or less the same as the number of plains. Of course that’s not possible, when playing 17 lands.
Should I prefer 9 islands and 8 plains over 8 islands and 9 plains? To answer this question, I have to focus on the cheap cards. The expensive cards shouldn’t be a problem because it is very unlikely to be unable to cast an expensive card due to color problems at the time you have enough mana for it as long as your mana base is reasonable. E.g., it should not be a problem to cast Prognostic Sphinx when I have 5 mana available.

In this kind of deck, my win-strategy is to cast early creatures and ordeals. So I have to make sure that I am able to cast cards like Phalanx Leader, Battlewise Hoplite, or Wingsteed Rider as soon as possible. Other cheap cards like Aqueous Form or Gods Willing are typically not early-game plays, so they are less important for my mana base planning.
Finally I decide to play 9 plains and 8 islands, because of the double mana symbols in important cards such as Wingsteed Rider and Spear of Heliod.
Let’s go through another example:

Clearly this is a less focused, weaker deck.

It plays more white (13) than blue (10) cards. The early game is stamped by the white cards, while most of the blue cards are late-game cards. My conclusion: Play 10 plains and 7 islands.
One last example:

Here I was very short on playables and had to add a black splash to the deck. Especially without any mana fixing, this will be a interesting mana base.

There are 6 blue cards (including Shipwreck Singer), 3 black cards, and 14 green cards. Additionally we have to consider that the 4 Agent of Horizons are most useful with blue mana.
Take a moment to think that through. What number of swamps, forests, and islands would you play?
Optimality of a Mana Base
Let me summarize what I usually think about when trying to find the right mana base:
- How many cards do I have in the different colors?
- Sometimes it’s useful to check the number of mana symbols, too.
- Is a color dominant in the early game?
- Are there any off-color activated abilities?
Now my intention was to find a mathematical way to put most of these questions into one number. I wanted to calculate a statistic that answer to the question “How good is a chosen mana base for a specific deck?” Therefore I answer the following question for every single card x in my deck:
Assuming card x is in my starting hand, for a given mana base, what is the probability to cast card x as soon as possible?
Take my first example. I want to answer the following questions:
- (1) What is the probability to cast Hopeful Eidolon on Turn 1, playing 9 plains and 8 islands?
- (2) What is the probability to cast Favored Hoplite on Turn 1, playing 9 plains and 8 islands?
- (3) What is the probability to cast Battlewise Hoplite on Turn 2, playing 9 plains and 8 islands?
- (4 – 22) …
- (23) What is the probability to cast Prognostic Sphinx on Turn 5, playing 9 plains and 8 islands?
This probabilities can be calculated by using a multivariate hypergeometric distribution. In the end I will have one probability for each card in my deck. These probabilities can be summarized by taking the product of the following over the whole set of them:
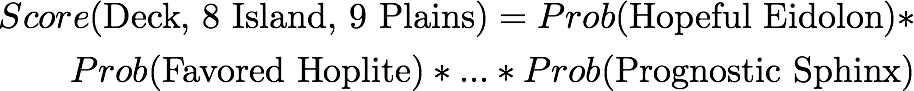
The resulting score measures how good a land-distribution is for a given deck. If the score is close to 100, then we have a very good chance to play any card in my deck as soon as possible. The smaller the number is, the less likely it is to be able to cast the right spells early.
Doing this for all possible combinations of basic lands, I am able to measure this quality for all of them. Just choose the one with the largest score.
Too complicated to do this on the fly?
Of course it’s a lot of work to go through this every time you do a draft. I needed a fast way to go through this. So I wrote a small web application which is doing the math for me. Let me show you how to use it:
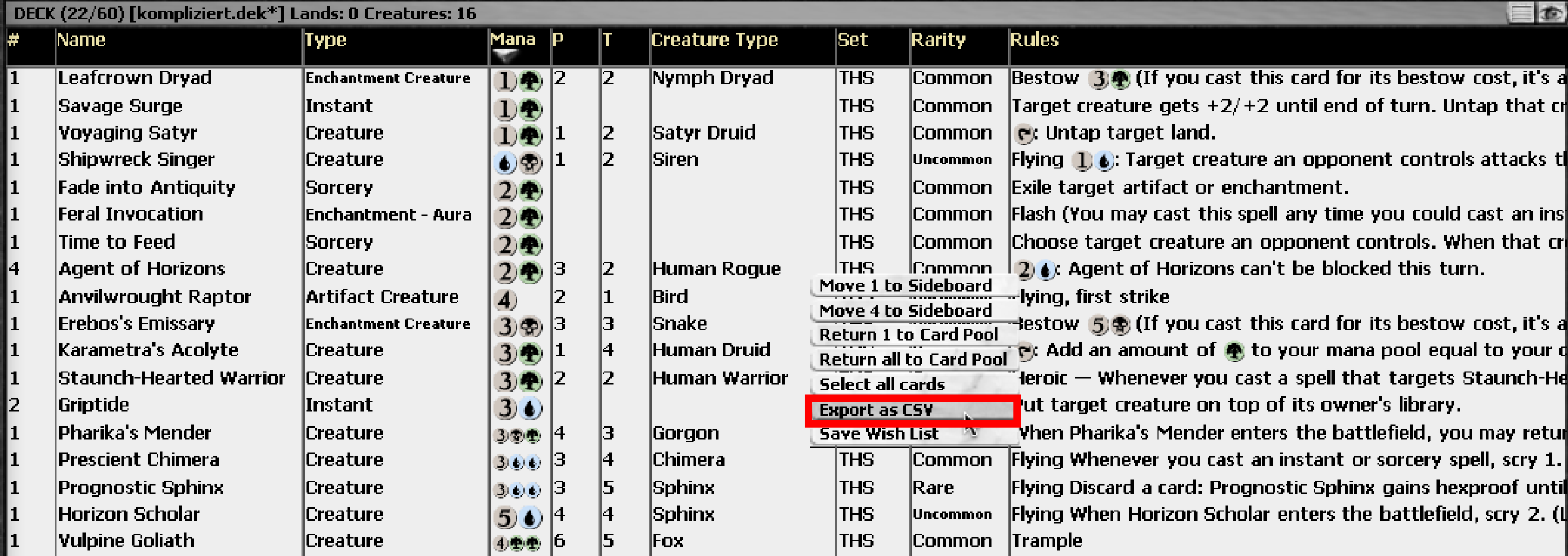
The first step is to save your decklist as a .csv file. This can be done by changing to the list view in Magic Online. Select all the cards in your deck and right-click somewhere on the selection. You will see in the context menu an entry to “export to .csv”. Save the file somewhere on your machine. You will need it in the next step.
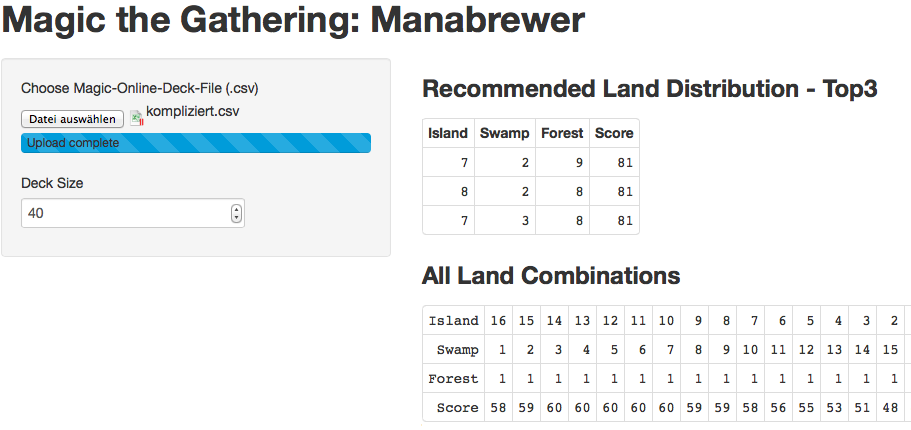
As a second step, follow this link and upload your deck list using the “Upload” button. The application will do the math and display the best 3 land distributions for your deck.
The first part shows the three highest recommended basic land combinations. Playing 7 islands, 2 swamps, and 9 forests achieves the largest score for my 3rd example. Playing 8 islands, 2 swamps, and 8 forests, or 7 islands, 3 swamps, and 8 forests seem to be similarly good, as the resulting score is 81 as well.
The second part of “All Land Combinations” gives an overview of all the other possible basic land combinations.
Conclusion
For most decks I tried, the web-app and thus my optimality criteria, produced very reasonable recommendations. Here are the results for the three discussed examples:
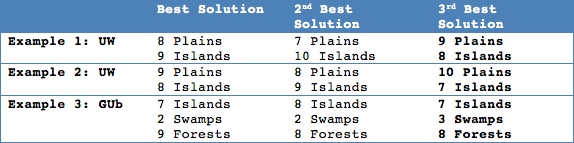
The top 3 recommendations are usually very close to each other in terms of my score. Here I played the 3rd best solution for each example because the statistic does not covering everything I want to take care of when planning my mana base.
Thus, be careful with how you interpret the results. The application does not know Magic. It is just crunching some numbers. In my first example, the app is calculating the probability of casting Gods Willing on Turn 1, which is not a reasonable play at all. The application is not able to replace thinking. But it might give you a good starting point for your evaluation.
Furthermore the app does not incorporate any mana fixers into its logic. So if you have any Traveler’s Amulets in your deck, the app is going to ignore it for the moment. The same applies for all lands producing more than one kind of mana (e.g., the scry lands).
I still have some more ideas to improve the app, which might result in some changes in the near future (e.g., support other sets than only Theros, allowing the user to add a weight for each card — so that, for example, one can manually decrease the importance of playing Gods Willing on Turn 1).
But in the meantime: If you like the idea, give it a shot! Try the app and send me some feedback (bugs, feature requests, etc.)!

Well, neither 2 nor 3 swamps is reasonable for the number of cards that would be dead if you drew no swamps, so perhaps starting from there makes sense?
Also, the general rule is that creatures are on-curve and spells are not, so separating those two would also make sense if you really want to accomplish much more than the MTGO default land suggester.
3 swamps seems doable, if not ideal. < 50% chance of drawing a card w/black that you can't play. The shipwreck singer makes it all a lot more awkward since having a dead 2-drop in hand is pretty bad, but on the other hand at least the singer can still be a good play in the mid-to-late game depending on board state. I would have gone with 9 Forests, 3 Swamps, 5 islands probably, though maybe 8 forests, 6 islands is better. I don't see how you run less than 3 swamps though.
Hey Noobeman, Hi Chris, thanks for the feedback.
I totally agree that 2 swamps seem to be way to few.
Actually the reason that my approach is recommending such a small number of swamps is that each card has the same relevance (so this is about what you are saying noobeman): The accumulated lower probability of playing any green or blue cards (20) on curve has just more impact when playing 4+ swamps than the increased probability of playing one of the three black cards.
Of course one could (and should!) argue if this approach is correct. But I think it is a reasonable starting point. Especially as any software will have a hard time to determine which cards are more or less important to play on curve. But I am working on a solution to change the time you want to play single cards of your deck manually (like Marshall likes to do it in his videos). Then we will be able to get even more sophisticated solutions.
In the meantime this has one great pro vs. MTGOs recommendations: We know what is happening inside.
Hi again, thought some more about the subject. I don’t think you should be multiplying those probabilities. They don’t and in many cases can’t happen at the same time. Perhaps start by just summing them up and try to adjust the formula from there?
The last deck is a very interesting example by the way. It is quite obvious that it’s impossible to build a proper mana base for it, so it’s a case of doing the best possible. I probably would just go for 8 forest 6 island 4 swamp, but I can see cutting a forest for a swamp just fine. Playing with 3 sources for 4 cards is madness, I would rather play with 19 or 20 lands instead, which is actually more likely to be correct.
Also, you have 3 cheap-cost double white things in first example. That should give more white than blue, certainly not 7 plains 10 islands, since the probability to cast those on curve goes down sharply with each plains removed. Imo, that indicates something is wrong with the premise itself – perhaps the formula.
Hey Noobeman: I really appreciate your feedback! Thanks!
1. Why multiplication instead of taking the sum of the probabilities?
At the start I made the whole thing the way you suggested it. The result was, that taking the sum leads to non plausible results for splashes. Splashed cards will always have a lower probability to be played on curve. But on the other side they tend to be more powerful. So we cannot accept a too low probability for them.
Now if you take the sum of the probs one card may have a very low prob as long as all the other cards have high probs and the resulting score will still be fairly high. But if you take the product a single very low prob will lead to a very poor overall score. E.g.:
(0.9 + 0.9 + 0.9 + 0.1)/4 = 0.7 while (0.9*0.9*0.9*0.1)^(1/4) = 0.52
Thats why I prefer the product: It forces a better prob. for every single card in the deck as it is more sensible vs. outliers.
2. You are talking about 4 black cards. I think you got that one wrong, as there are only 3 black cards in that example.
3. I’ll definitely check the code for the first example again. As you mention it I have to agree that the recommended results seem to be too “blue”.
1) It is true that, at first glance, the multiplication formula should give the proper result. I will be honest and say that I suggested taking a sum without giving it much thought, the logic being: wrong result means wrong approach to getting said result. Now that I think about it, the formula should give the proper answer – but it clearly doesn’t, as example 1 shows.
2) My mistake, in that case 4 sources is sort of acceptable.
Splashes and the required manabase are an interesting topic in general. People often talk about “1 more source than you have spells”. A recent episode of Simon Says on this site discussed this problem as well. The conclusion seemed to be that even with 1 card splash you are far better off with 3 sources than 2, and with larger splashes it quickly gets ugly, a 3 card splash requiring something crazy like 6 sources to be reasonably certain of getting the mana in time.
There is also the issue that after a certain number of lands (around 6-8) you can assume you will draw one land of this type in every game. And this gets into a weird relationship with the first conclusion. =)
This is why I am curious to see the results your approach will bring. Even if it brings nothing tangible, it is certainly fun to try.
The number one problem right now is of course that even on a simple example (the first one), the results do not match the expectations.
It is possible that higher average CMC of blue cards means that their probability is easier to max with lands, leading to skewed results.
Hey, sorry for my late reply. I’m quite busy at the moment but I will check the web app asap and post when I found the reason for the strange results in case 1!
I will for sure go deeper on this and try to enhance the app with more sophisticated functions. We’ll see how useful it can become!